領域概要

本領域は計算複雑さの理論において，今後の研究の指針となる新たな研究の流れを創出することを目標とする．計算複雑さの理論の中心的課題は，我々 が処理したい仕事や解きたい計算問題に対し，「これ以上の効率化は不可能である」という限界を見極めることである．効率の良いアルゴリズムをとことん追究 するアルゴリズム論と両輪を成す理論計算機科学の重要な研究分野である．

計算複雑さの解析の重要性は，コンピュータの出現当初から認識されていたが，計算量の概念の確立（1960年代），クラスNP等の重要なクラスの 導入（1970年代），乱択計算や一方向関数などの研究，回路計算量での下界の証明（1980年代），対話型証明の導入とその発展形であるPCP定理の確 立（1990年代）などを経て，現在，様々な解析技法が提案されてきた．そして今世紀に入ってからは，米国 Center for Computational Intractability の発足などもあって，様々な解析技法が究極的に研ぎ澄まされてきている．

しかしその一方で，重要な未解決問題が山積しており，現時点では，その攻略法も見えていない．その典型的な例がP≠NP予想である．たとえば，典 型的なNP問題に対して，我々は指数関数的計算量を持つアルゴリズムしか得られていないし，多分，それが限界だと予想されているが，多項式時間どころか， 線形時間では計算できないこと（正確には，非線形サイズの回路計算量下界）すら証明されていない．

こうした現状を打開するためには，種々の未解決問題解決までの道筋を示すような強力な研究シナリオが必要である．そのシナリオ作りが本領域の大き な目標である．この目標は遠大であるが，近年，世界中の研究者の英知の結集により徐々にそのための階段が築かれつつある．たとえば，P=BPP予想に対し ては，擬似乱数列生成の研究から始まった研究の積み重ねにより，計算困難性との結びつきが明確化されつつある．また，最新の解析技法と新たなアルゴリズム 手法を組合せることで，NEXP not⊆ ACC0という未解決問題も2010年に証明されている．様々な解析技法はそこまで進化してきたのである．我々は，こうした解析技法や計算の特徴の研究を 多面的に理解し，その関連を深く掘り下げ，その中から課題解決へ向けて，これらの組合せで何ができるのか，またさらに何が必要なのかを見出していく．

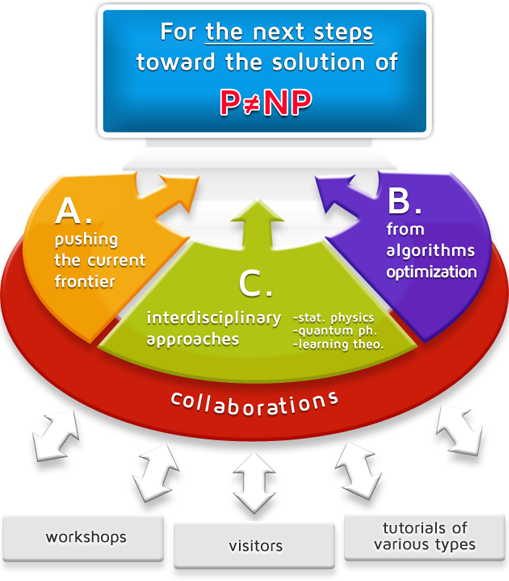
以上のような研究を進めるため，本領域では3つの異なる観点から研究を進める計画班グループを編成した．Ａチーム：各々主要な解析技法を徹底的に 追究する3つの計画研究班，Ｂチーム：スパコンをも利用した新たな計算限界解明手法の開発やその展開に挑む3つの計画研究班，Ｃチーム：境界領域の視点で 新たな考え方や解釈を見出すことを目指す3つの計画研究班，である．新しい計算限界解明手法は，計算の新たな見方を提供するが，それは場合によっては画期 的なアルゴリズムに結び付く可能性もある．Ｂチームの1つの班は，そのような計算限界解明手法の実用分野への展開を目指した研究も行う．また，こうした計 画班の連携の要として，「計算限界研究センター (Center for Exploring the Limits of Computation, CELC)」を創設し，若手研究者や多数の訪問研究者などを軸に，各班の研究者間の連携を推進していく．また，公募研究も25年度開始の研究を10件程度 公募する予定である．

より詳しくは，電子情報通信学会 コンピュテーション研究会での講演資料 『 新学術領域「計算限界解明」発足にあたって』 をご覧ください． また、計算量理論への入門編として，ELC Complexity Theory Intro. Seminar Series を公開していますので， こちらも併せてご覧ください．

組織について

　総括班
　　　・研究の総括
　　　・各種事業の企画と運営
　　　・計算限界研究センター CELC の運営
　　　・訪問研究者の招聘
　Ａチーム：計画研究3班，公募研究?班
　　　・最も注目されている解析法や対象問題の徹底分析
　　　・限界解明フロンティアの開拓
　　　・領域で共通に議論するテーマの提供
　Ｂチーム：計画研究3班，公募研究?班
　　　・計算上界（アルゴリズム開発）からの計算限界解析法の開発研究
　　　・スパコンの計算限界解明への応用
　　　・限界解析法からアルゴリズムへの展開
　Ｃチーム：計画研究3班，公募研究?班
　　　・境界領域からの計算限界解析法検討
　　　・異分野境界領域からの解析法の開発
　　　・限界解析技法に対する別解釈の提供
　計算限界研究センター
　　　・招聘研究者のホスト
　　　・PDのホスト
　　　・定期セミナーの主催